

2008-06-19 21:37:00
One of the few second year's courses that I got out of the way in my first year at college is History 2, ie Geschiedenis 2 - Vakgedeelte. I'd planned on leaving the didactical part of the course until the next year.
The workload for this course isn't that high and it mostly depends on the students reading a whole book on the history of mathematics. Starting at the arithmetic of the Egyptians and Babylonians we proceed through India, Arabia, the middle ages and the Renaissance to discover how maths evolved through the ages. Surprisingly most of the really interesting stuff starts around the seventeenth century. -Astoundingly-, over 90% of the maths we know was invented after 1900. o_O
As part of the preparations for our exam, each student was asked to write a two page biography of a famous mathematician. I was assigned Euclid (Euclides in dutch).
This document is available as a .PDF document and can be downloaded here.
This course relies on a syllabus made by the Hogeschool and the Math through the ages book by Berlinghoff and Gouvea (Amazon.com). Since the book's rather voluminous I reckoned I'd write a summary of the whole thing, with some stuff from the syllabus thrown in.
This document is available as a .PDF document and can be downloaded here.
One of the minor assignments we were given was to work out a few ancient, dutch math assignments. Well, ancient? Sixteenth, seventeenth century like-stuff. It was actually fun to try and decypher the instructions given in the original texts.
This document is available as a .PDF document and can be downloaded here.
kilala.nl tags: school, teaching, summary, maths,
View or add comments (curr. 0)
2008-05-06 21:51:00

A few weeks ago I wrote about my research on Euclid, the ancient Greek mathematician. Said research wasn't anything noteworthy, just something to form a basis for a biography written for a school assignment.
Back then I also wrote about a man called Richard Fitzpatrick and his remarkable work. You see, Mr Fitzpatrick took a nineteenth century translation of the Elements of geometry by Euclid and reworked into a new book. Each page of this book is split in two: one column with a greek text approaching the greek original and one column with a modern english translation. While the greek text doesn't add much for the budding mathematician, it does add a definite factor of "cool" ^_^
Mr Fitzpatrick's book can be downloaded for free as a PDF, but you can also buy a printed version from Lulu.com. Lulu.com allows you to publish your own books at a very low price, which many academics and aspiring authors put to good use. $27 (including S&H) bought me a beautiful, hard cover book with an accessible translation of Euclid's Elements. The sleek, black cover looks quite nice and the fact that the book is printed on A4 paper makes it very easy to read.
Now... I shot some video while leafing through the book, just to give you an impression. The video came out a bit blurry, but that's what I get for using my compact camera under fluorescent lighting ^_^;
kilala.nl tags: school, awesome, internet, maths,
View or add comments (curr. 0)
2008-04-21 09:28:00
Analysis 1 - Didactics is one of the larger projects that the first year's students have to tackle. There are ten reports to be made, some of them rather largeish. To us the project is known as Analyse 1 - Didactiek - Rekenen is complex. Analysis in this case is the dutch name for what is know in the english speaking world as Calculus.
In short, this course focusses on the learning of arithmetic and math. We'll take close looks at the various algorithms that children need to learn and we'll even try and re-learn calculus ourselves by doing it all in Base-8 (octal). I found this class particularly challenging, mostly due to the pressure of having to hammer out these reports so quickly. All in all I did well though, since I managed to score a 90% at the end of the term :)
Students are asked to re-learn arithmetic by doing it all in Base-8, instead of in Base-10. This way we would be forced to study addition, subtraction, multiplication and division like we were twelve year olds again. This was great fun! We also examined multiple methods to do multiplication.
This document is available as a .PDF document and can be downloaded here.
All of us are studying to become math teachers in high school, so it's only natural for us to focus on maths for teenagers. However, it is also a very interesting exercise to examine mathematics education in pre- and middle school. Using reports made by CITO called the PPON (Periodieke Peiling Onderwijs Niveau, more information here), we are asked to investigate the level of math knowledge at the end of preschool (K8 in the USA). We are also asked to search for any problem areas that our teenagers may have encountered in their education.
This document is available as a .PDF document and can be downloaded here.
One of the (comparatively) recent trends in mathematics education is realistic calculation (realistisch rekenen). The proponents of this method reason that students don't benefit from simply repeating algorithms all day. Instead, they'd like assignments to relate to reality by way of providing a context. That ought to keep students motivated, while also keeping maths "tangible" for them.
For this report, students are asked to investigate the pros and cons of realistic maths.
This document is available as a .PDF document and can be downloaded here.
This assignment is kind of similar to the first report: we will be re-learning various methods for division and for determining the square root of a number.
This document is available as a .PDF document and can be downloaded here.
Remedial teaching is an important part of education. Not every child will immediately grasp the concepts that you are explaining and some will have a downright hard time understanding the materials. As teachers we will need to understand why students make the mistakes they do and we'll need to know how to address these problems.
For this assignment we'll be talking with kids, after taking a look at some of the mistakes they've made in their calculations. For my report I spoke with a few kids who'd recently done a test on coordinates.
This document is available as a .PDF document and can be downloaded here.
Continuing the research into thinking mistakes, the student is given five separate situations to analyse. In each, people have made mistakes in their assumptions or calculations and it's up to the students to find and explain them.
This document is available as a .PDF document and can be downloaded here.
The students are asked to do some book research on learning disabilities and disorders that may affect kids in learning mathematics.
This document is available as a .PDF document and can be downloaded here.
For this assignment students will treat the high school math education as a black box. We will be comparing the output of pre school with the output of high school to determine the process that takes place -in- high school. As input for our research we will be using the final exams of preschool and the final exams of maths education in the VMBO part of high school.
This document is available as a .PDF document and can be downloaded here.
We continue our research of realistic math by researching contexts used to teach about negative numbers. This is one of the notorious subjects in teaching high school maths.
This document is available as a .PDF document and can be downloaded here.
For our final report, we are asked to do a didactical analysis (didactische analyse) of the way that fractions, percentages and decimals are taught in high school. This starts off with some book research and ends with us pouring through books for the first three years of maths ed in high school. Nice :)
This document is available as a .PDF document and can be downloaded here.
kilala.nl tags: school, maths, summary,
View or add comments (curr. 0)
2008-04-20 14:16:00

This semester I'm taking the second year's course Geschiedenis 2 Vakgedeelte, which can be translated as History of math 2. Over the next two months we'll be taking a look at math through the ages, starting with the Egyptians and Babylonians.
As part of this course, each student is expected to write a short biography on one of the Great Mathematicians (tm). I was assigned Euclid (Euclides in dutch), which seems to be a very interesting topic. So far I've done some six hours of research and I've gotten a pretty good picture so far.
During my research I've run into some very cool things! Things that may be of interest to a lot of people :)
For instance, there's Rare Book Room.org. This website has gathered thousands and thousands of photographs of antique books. They've created a huge archive, so that mere mortals such as you and I can leaf through tomes that are normally in musea.
A 1482 print of Elements, by Euclid.
A 1613 print of Istoria e Dimostrazioni Intorno Alle Macchie Solar, by Galileo Galilei.
Another neat project is Euclid's elements of geometry by Richard Fitzpatrick. Mr Fitzpatrick has taken the 1883 Heiberg translation and used it to make a completely fresh english translation of Elements (Euclid's most famous work). You can download the book for free as a .PDF at the link provided, or you can fork over $28 to buy the hardcover print from Lulu.com. I'd say the print is definitely worth it! I've just ordered my copy, to support Mr Fitzpatrick's work.
kilala.nl tags: school, studying, maths,
View or add comments (curr. 0)
2008-02-05 22:36:00
Here's a little taster of the stuff I'll be using in Thursday's math class. I'll be introducing the kids in a VMBO-BL class to the notion of negative numbers, which can be quite a challenge. I mean, how the heck do you explain to a twelve year old that there's something smaller than zero?
Of course, people will immediately point out things like temperatures, debt and years B.C. Thing is, those are only examples of negative numbers and they don't explain how or why. They just show that it's possible, but a child may not instinctively understand how these figures work.
So, this should prove to be interesting! The picture shown above is part of a stencil I'm putting together for the students. It's part of the first assignment they'll be making, pointing out the height at which various objects reside. I'm very curious about how it'll work out :)
kilala.nl tags: teaching, school, creative, maths,
View or add comments (curr. 2)
2008-02-02 08:41:00
Or apparently that's what prof. DeTurck of Penssylvania-U thinks.
DeTurck does not want to abolish the teaching of fractions and long division altogether. He believes fractions are important for high-level mathematics and scientific research. But it could be that the study of fractions should be delayed until it can be understood, perhaps after a student learns calculus, he said. Long division has its uses, too, but maybe it doesn't need to be taught as intensely.
From:
and
Of course, like many others I believe this notion to be nuts. Decimals have no meaning unless you know what fractions are. It'll be like handing a bunch of powertools to a carpenters apprentice and asking him to build a house. Oh, you don't need to know what everything does, just get to work...
As a future maths teacher I'm scared by this idea. And it's not just limited to the US. A dutch prof by the name of Kees Hoogland shares DeTurck's opinion that kids should be learning less longhand maths and should instead be focusing on using the calculator. Why? Because they'd be stupid not to use the modern materials at their disposal. *sigh*
I've started a forum discussion about this, over at Ars. Obviously, it's gotten some pissed off responses ^_^
EDIT:
In response to my thread over at Ars, GwT has started a new thread asking how important math is in general.
kilala.nl tags: school, studying, weird, maths,
View or add comments (curr. 0)
2007-11-17 11:55:00
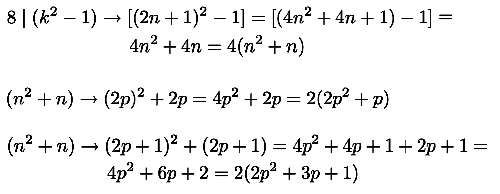
Careful now, this may sting a little... o_O
This semester we're covering Analysis 1, which requires a wholly new way of thinking. Where Statistics 1 was pure maths and calculation, this course requires something additional: insight and a sense of logic.
The thing about this course is that it's all about proving maths. Not using maths to prove stuff, but proving the mathematic equations themselves.
Folks who aren't too hot on math may want to skip the next section :D
==========
For example, the calculation show is above belongs to the question "Prove or disprove that (k^2 -1) is divisible by eight, for all values of K that are integers and odd". "Odd" in this case is opposed to "even".
So, how do you even get started on such a question?! Well, you start filing in bits and pieces, starting out by equating k to (2n + 1). Why? Because one can make -any- odd number by taking integer n, multiplying it by 2 (thus becoming an even number) and then adding 1.
Once all of that is done we're left with 4(n^2 + n). In order for the original theory to be right, this'd mean that any value of (n^2 + n) needs to be even. And that's what I'm testing in the second and third lines: first for even numbers, then for odd numbers. And indeed, both tests come out positive: any value for n will result in an even number.
Pulling this back to the original theory means that any outcome is indeed divisible by eight, because four times any even number is always divisible by eight.
==========
Joy!... I've always sucked at being insightful, so a lot of these "tricks" don't come natural to me. Then again, I used to get good grades for math and even for stuff like this. I ought to be able to get the hang of it again.
I hope ^_^;;
kilala.nl tags: school, studying, maths,
View or add comments (curr. 1)
2007-11-02 11:51:00
I assume that it's Hogeschool Utrecht's philosophy to start their students off with basic knowledge that can be applied in practice, followed by years of more advanced information. This methodology has irked quite a few of my classmates, but I really don't mind. I actually quite like it.
One of the more advanced courses (it's a second year's class) is Vakproject Vakdidactiek 2 (General & Maths didactics 2). This course is divided into two separate streams: one covering general didactics for the complete n00bs (like me) and one covering didactics in maths. The first stream is finalised with an exam, while the second stream requires the student to write a full dozen (12!!!) reports.
I have already written summaries on general didactics, which can be found on this page and on this page. The page you're currently browsing features -all- of my term papers for the maths didactics part.
At the start of this second year's course we are asked what we believe makes a "good" maths teacher. We are asked to analyse our own strengths and weaknesses, so we can form goals for ourselves.
This document is available as a .PDF document and can be downloaded here.
This report is based on BIT-report 1. What's different is that dossier opdracht 2 also contains my description of the lessons I've drawn from the course material.
This document is available as a .PDF document and can be downloaded here.
We've already discussed direct instruction on earlier occasions (BIT-report 1). For this assignment, students are expected to design a class plan on the subject of the Pythagoras theorem.
This document is available as a .PDF document and can be downloaded here.
After working on dossier opdracht 3, students are asked to review each other's work in pairs. Report 4 contains the feedback that I've given one of my class mates.
This document is available as a .PDF document and can be downloaded here.
Term paper 8 requires that I spend some time teaching a class. Unfortunately I haven't been able to do that yet. Hence, there's no paper for you to review.
This one's a huge one, weighing in at around thirty pages! We are asked to take an exam that's been handed out in class and turn it inside out. What's wrong with it? What's good about it? How would you grade the paper?
We are also given five tests as they were turned in by students. What did they do right? Where did they go wrong? Can you understand why they made certain mistakes?
This was a very interesting assignment, but IMHO it was just too fscking huge. I sank at least thirty hours into this report.
This document is available as a .PDF document and can be downloaded here.
Term paper 7 requires that I spend some time teaching a class. Unfortunately I haven't been able to do that yet. Hence, there's no paper for you to review.
Term paper 8 requires that I spend some time teaching a class. Unfortunately I haven't been able to do that yet. Hence, there's no paper for you to review.
This assignment focusses on the problems high school students may encounter when using the dutch language. Students are asked to read and analyse a few chapters on this matter.
This document is available as a .PDF document and can be downloaded here.
This assignment focusses on the problems high school students may encounter when using the dutch language. The object is to analyse an assignment that would've been used on an exam, to find its flaws and to rewrite it.
This document is available as a .PDF document and can be downloaded here.
This assignment focusses on cooperative learning, as pioneered by Dr. Spencer Kagan. It contains a summary of relevant chapters from our course books, as well as a BIT reading report.
This document is available as a .PDF document and can be downloaded here.
This assignment focusses on cooperative learning and takes a look at Wiki's as a learning tool.
This document is available as a .PDF document and can be downloaded here.
kilala.nl tags: school, maths, summary,
View or add comments (curr. 0)
2007-11-02 10:30:00
The first year at Hogeschool Utrecht's study Tweedegraads docent wiskunde starts you off with a course in statistics. They could've picked any part of math to start out with, but it was this one :)
The course, Statistics 1, is divided into two classes: one dealing with the actual maths, the other dealing with the didactics involved with teaching statistics. The first class ends with an exam, while the second requires you to hand in a total of eight papers (called dossier opdrachten. This page serves as a portal to all eight of my reports.
As their first assignment of the year, students are asked to investigate how statistics are taught in high school. We are asked to focus on the first three years of HS, thus limiting the scale of the job.
Each student picks one specific method and searches through all the books for those three years. Any mention of statistics should get a little footnote, while whole chapters on statistics deserve a thorough analysis. For my report I picked the Getal en ruimte method.
This document is available as a .PDF document and can be downloaded here. Be aware that the file is a whopping 10MB, due to the heavy use of images.
In a similar light as the first paper, students are asked to investigate the final terms for statistics. The VMBO have a list with specific subjects from statistics that should be featured in the exams. We are asked to pick one assignment per subject from the method we used for the first paper.
This document is available as a .PDF document and can be downloaded here. Be aware that the file is a whopping 6MB, due to the heavy use of images.
One of the many philosophies in teaching is direct instruction (directe instructie). One of the key principles of this philosophy is that one should keep student motivated. Motivated students are willing to accept education and will thus learn more efficiently. For more information on direct instruction, read BIT-report 1 on maths didactics.
In order to grasp students' attention it's good to start a class with a bang. We were asked to write three separate opening sessions (15 minutes each), which can be used in a class on statistics. One of these openings will be presented in class. For a report on these presentations, read my class notes for weeks 3 through 5.
My class openings use the following subjects:
This document is available as a .PDF document and can be downloaded here.
After giving the presentation mentioned with dossier opdracht 3, each student is given feedback by his classmates. Feedback is gathered through forms created by the student and through forms handed out by the teacher.
Dossier opdracht 4 gathers all the feedback into one report, for analysis. It's expected that I use this report as a guideline for future learning goals.
This document is available as a .PDF document and can be downloaded here.
In teaching statistics, schools often make a grab for software like MS Excel and VU Stat (or SPPS). For this report, students are asked to investigate the capabilities of these tools and to assess their usefulness in teaching statistics.
This document is available as a .PDF document and can be downloaded here.
For paper 5 we researched software that runs on the local computer, like Excel and VU Stat. With paper 6 we are asked to research online tools. One may not expect this, but there are a few websites out there that offer schools online learning suites.
This document is available as a .PDF document and can be downloaded here.
The students are asked to investigate GWAs. In this case, GWA stands for Geintegreerde Wiskunde Activiteit (Integrated Maths Activity). The idea behind GWAs are that they're supposed to help students discover the place math has in daily life.
GWA assignments pose the student a problem and give no hints as to the required theory. A student is expected to figure things out by himself. He'll need to discover which pieces of theory are required and how he should combine them.
Our investigation quickly glances over the how-and-why of GWAs. One of the most important conclusions of the report are five characteristics that a "good" GWA should have.
This document is available as a .PDF document and can be downloaded here.
As you may have read, dossier opdracht 8 gave me quite a bit of trouble.
The students are asked to create a GWA for students in their first, second or third year of high school. My report covers a GWA on electronic payments (electronisch betalen).
This document is available as a series of three .PDF documents. Part 1. Part 2. Part 3.
kilala.nl tags: school, maths, summary,
View or add comments (curr. 2)
2007-10-14 11:06:00
Statistics seems to be one of the least liked subjects among students taking maths as part of their curriculum. This seems to be the same in both high school and college. I'm not entirely sure why this is, but I've heard a lot of people call the subject matter vague and the rules fuzzy.
The HU must've thought it'd be good to start off with this tough subject, 'cause that's what they dropped on us for the first semester :) STAT1-VAK is one half of the Statistics course, the other half of the course focussing on didactics. STAT1-VAK is closed off with a test of three chapters on statistics, taken from the Moderne Wiskunde books.
This summary focuses on the following chapters from the Moderne Wiskunde books.
You can download the summary as a PDF document.
kilala.nl tags: school, maths, summary,
View or add comments (curr. 0)
2007-09-26 13:51:00
In my first year at Hogeschool Utrecht I will follow a few second year's courses, to speed up my studies. One of these second year courses is Project Vakdidactiek, which concerns the didactics behind teaching maths.
The final term for this project consists of a dozen reports and assignments, all of which should prove your comprehension of didactics. Materials used in this course include Effectief leren in de les by S. Ebbens e.a. and Wiskundeonderwijs in de basisvorming by APS Publishing.
A few of the assignments require us to make so-called BIT leesverslagen (reading reports). These reports include a summary of the relevant chapters, as well as a chapter covering reflection on the material. On this web page I'll publish the summary sections of these reports. I'll keep the other stuff to myself for now.
Currently, summaries for the following chapters are available.
This is part of dossieropdracht 2, which focuses on direct instruction (directe instructie).
You can download the summary as a PDF document.
This is part of dossieropdracht 11, which focuses on cooperative learning (samenwerkend leren).
You can download the summary as a PDF document.
kilala.nl tags: school, summary, maths,
View or add comments (curr. 0)
2007-09-22 11:46:00
For one of my school assignments I was asked to write three class openings for the subject of statistics. The object of a class opening is to draw in the students, to capture their attention and to motivate them.
The opening I presented at school involved the McNuggets problem (aka the Frobenius problem). It was well received, though most of my class mates thought it better suitable for a class on analytical math. I tend to agree with them now.
One of the other openings I've designed involves the famous Monty Hall problem. The one that involves a gameshow, three doors, two goats and a car. Ring a bell?
Because this problem is so counter-intuitive it tends to throw a lot of people off. Their gut instinct tells them that the chance of winning a car (after revealing one of the goats) should be 50%. They are unfortunately incorrect.
Before we continue, some of you may enjoy a snippet from the TV show Numb3rs. The character of Charlie Eppes doesn't explain the solution very clearly, but does make a nice job of explaining the problem.
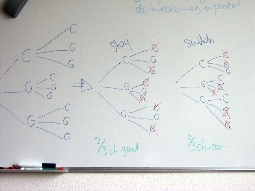
I tried to come to the proper solution by myself by using a decision tree (boom diagram in dutch). It took me a while, but I got there :) My tree looks a bit different from the one Wikipedia shows (linked above), but that's because I use two trees instead of combining them into one.
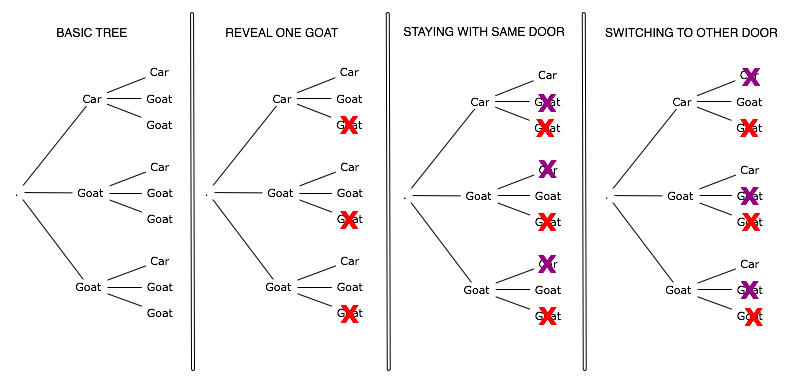
Going from left to right:
* The original tree, unconstrained, given that you get two choices.
* The gameshow host takes away one of the goats. He asks you whether you want to switch doors.
* The decision tree, should you stay with the door you chose.
* The decision tree, should you decide to switch doors.
The red X-es show the option taken away by the host. The purple X-es show the option taken away by your own choice.
Yes, it's counter-intuitive, but switching doors after having one goat revealed IMPROVES your chances. Instead of having a 1:3 chance, you now have 2:3! Nice!
And this is why I think this problem would make a nice opener for a high school course on statistics. It stumps the kids, makes them curious and them amazes them :)
kilala.nl tags: school, geeky, maths,
View or add comments (curr. 0)
2007-08-31 07:00:00
Last night was the school year's official opening at Hogeschool Utrecht. Around 17:00 all aspiring tweedegraads teachers gathered in the cafeteria for a speech from the rector. It was interesting to see that the group was both large and varied. I reckon there were about a hundred people there, maybe one-twenty. Aged between twenty and somewhere in their fifties I saw a lot of caucasians, mixed in with a few turks and moroccans.
One startling realization was the fact that almost 50% of the group were there for the same degree I was after: tweedegraads maths teacher. I guess either it's a popular passtime, or people have caught on to the fact that maths teachers are sought after. All in all there's sixty people starting the maths course this year. Wow!
After the whole introduction and a tour of the school building (which we'll be leaving come January, to move to a new one) there were drinks. I finally got the chance to meet some of my fellow students. It's slightly daunting to know that a whole bunch of them are already in education, but I'm not going to let that get in my way :)
So far they seem like a nice bunch of people! There's the strong-and-silent guys, the rowdy drinking-after-playing-footbal guys, the silent-and-mousy women and so on. There was also this one woman (I think she's in her forties though I'm horrible at guessing ages) who's great! She's absolutely bubbling with enthusiasm for the course! Kind of like how I felt after my intake with the coordinator :)
Yes. This is going to be an interesting year!
kilala.nl tags: career, school, teaching, maths,
View or add comments (curr. 0)
2007-08-14 21:36:00

Since school starts in about three weeks I thought it was about damn time to start getting prepared! It's one thing to make all arrangements with the school, taking care of paperwork and talking to people. But it's another thing entirely to actually be prepared for the course material!
I graduated from college a little over seven years ago. For about half of my college years I was very busy with maths, learning all kinds of new tricks. All the other time was spent programming, doing web design and learning about Unix. Since my career progressed with the latter half of what I just described, it's only natural for my maths to be a little rusty.
Well, rusty would be an understatement. Consider if you will one of the original, iron nails that Noah had used in his arc. Having been exposed to tremendous amounts of sea water and ages upon ages of time it's sure to be a bit rusty. Now, let's assume that ever since that flood the nail had been exposed to corrosives, acid rain and various other nasties. Not much would be left of it, right? A nasty, little chunk of iron would be all that's left.
Well, that's where my current grasp of maths is.
Thankfully I am confident that I can at least completely revive my high school math skills, considering this blog post. Back in 2005 I prepped Marlijne for an exam that consisted of all my HS maths in only a few hours.
Also thankfully, unlike what I wrote in that blog post, I did -not- throw away my math books! /o/
The picture above shows all of the books that I want to go through before school starts. The bottom row (plus the b/w book at the top left) are all high school books from my final two years. They cover everything from functions and equations, through trigonometry, to differentials and logarithms.
The top row is the stuff I went through in college. It's also the stuff that currently gives me a dread feeling in my stomach because it is way beyond me. They start out by repeating a little bit of HS stuff (differentials, functions), but then quickly move on to limits, logarithms, partial differentials, integrals, multiple variable equations and vectors. Zounds! I won't even mention the two other books that cover Laplace transforms and Fourier strains. Although I doubt whether I'll need to know any of that stuff.
Unfortunately I -have- thrown out all of my syllabi, meaning that I'm out of materials on chance calculation and on matrices. Luckily my friend The Saint is willing to lend me his copies. Apparently his storage space is larger than mine and he's hung onto most of the stuff from our college years ^_^
Well! Here I go! Study study study!
kilala.nl tags: studying, school, maths,
View or add comments (curr. 2)
All content, with exception of "borrowed" blogpost images, or unless otherwise indicated, is copyright of Tess Sluijter. The character Kilala the cat-demon is copyright of Rumiko Takahashi and used here without permission.