

2007-09-22 11:46:00
For one of my school assignments I was asked to write three class openings for the subject of statistics. The object of a class opening is to draw in the students, to capture their attention and to motivate them.
The opening I presented at school involved the McNuggets problem (aka the Frobenius problem). It was well received, though most of my class mates thought it better suitable for a class on analytical math. I tend to agree with them now.
One of the other openings I've designed involves the famous Monty Hall problem. The one that involves a gameshow, three doors, two goats and a car. Ring a bell?
Because this problem is so counter-intuitive it tends to throw a lot of people off. Their gut instinct tells them that the chance of winning a car (after revealing one of the goats) should be 50%. They are unfortunately incorrect.
Before we continue, some of you may enjoy a snippet from the TV show Numb3rs. The character of Charlie Eppes doesn't explain the solution very clearly, but does make a nice job of explaining the problem.
I tried to come to the proper solution by myself by using a decision tree (boom diagram in dutch). It took me a while, but I got there :) My tree looks a bit different from the one Wikipedia shows (linked above), but that's because I use two trees instead of combining them into one.
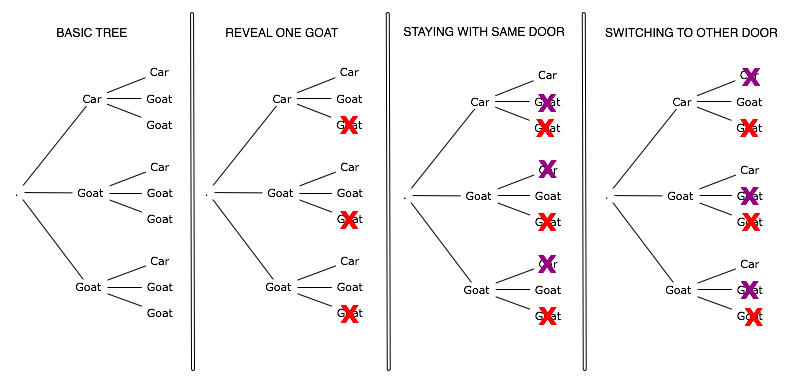
Going from left to right:
* The original tree, unconstrained, given that you get two choices.
* The gameshow host takes away one of the goats. He asks you whether you want to switch doors.
* The decision tree, should you stay with the door you chose.
* The decision tree, should you decide to switch doors.
The red X-es show the option taken away by the host. The purple X-es show the option taken away by your own choice.
Yes, it's counter-intuitive, but switching doors after having one goat revealed IMPROVES your chances. Instead of having a 1:3 chance, you now have 2:3! Nice!
And this is why I think this problem would make a nice opener for a high school course on statistics. It stumps the kids, makes them curious and them amazes them :)
kilala.nl tags: school, geeky, maths,
View or add comments (curr. 0)
All content, with exception of "borrowed" blogpost images, or unless otherwise indicated, is copyright of Tess Sluijter. The character Kilala the cat-demon is copyright of Rumiko Takahashi and used here without permission.